Maze Generation

Maze generation is a fascinating topic. There are many ways to generate mazes and each one of them generates mazes with its own unique properties.

In this blog post, I look some of the ways in which we can generate mazes. Before we can get into any of these algorithms, we must first figure out how our maze is modeled and stored inside our program.

Modelling the maze

To get started, we can think of our maze a n by n grid of cells where a cell contains information about its index in the grid.

Note: The cell can also contain references to its neighbors. This is helpful when you want to solve the maze using state space search algorithms like Depth First Search, Breadth First Search, etc.

Next, we need to be able to store which cells are connected, i.e., which cells do not have a wall separating them. For this we use what is known as an adjacency matrix. The adjacency matrix is a m by m grid where m is the number of cells in our maze = n2. In the matrix the value at row i and column j represents whether or not the cell i and cell j are connected or not.

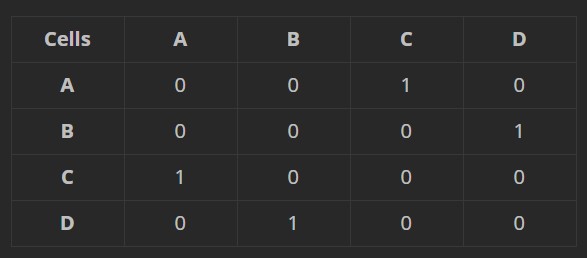
Here for example since A and C are connected, [A, C] and [C, A] are given the value 1.

This is essentially a graph data structure.

Now that we have a way to store our maze, we can start looking at some of the algorithms we can use to actually generate our mazes.

Generating the maze

We are going to look at the following algorithms:

1. Randomized Depth First Search algorithm
2. Randomized Kruskal’s algorithm
3. Randomized Prim’s algorithm

Randomized Depth First Search

Stack<Cell> backtrackingPath; // A stack to facilitate backtracking

// Pick random starting cell from grid of cells
startingCell = getRandomCell(grid);

// Add starting cell to backtracking path
backtrackingPath.Push(startingCell);

while(backtrackingPath.Count != 0) {
    // Get the cell to explore from the stack
    currentCell = backtrackingPath.Peek();

    currentCell.visited = true;

    // Get the possible neighbors of the current cell
    neighbors = getNeighbors(currentCell);

    // If all the neighbors have been viewed then backtrack
    if (getVisitedNeighborsCount(neighbors) == 0)
        backtrackingPath.Pop();
    else {
        // Select a random neighbor from all non-null and un-visited cells
        neighbor = neighbors[random.Next(n)];

        // Add selected neighbor to stack for backtracking
        backtrackingPath.Push(neighbor);

        // Remove walls between neighbor
        setNeighbor(neighbor, currentCell);
    }
}

Randomized Kruskal’s Algorithm

// A wall is essentially a pair of cells which are seperated
struct Wall { Cell c1; Cell c2; }

// To help us check for loops in maze
DisjointSet connectedCells;

List<Wall> walls; // List of all the walls

// Shuffle the order of the walls
shuffleWalls(walls);

foreach(wall in walls) {
    // Connect the cells divided by this wall
    // if are not indirectly connected
    if (connectedCells.find(getIndex(wall.c1))
        != connectedCells.find(getIndex(wall.c2))) {
        setNeighbor(wall.c1, wall.c2);
        connectedCells.union(wall.c1, wall.c2);
    }
}

Randomized Prim’s Algorithm

// A wall is essentially a pair of cells which are seperated
struct Wall { Cell c1; Cell c2; }

List<Wall> walls; // Empty list to store walls

// Pick random starting cell from grid of cells
startingCell = getRandomCell(grid);
startingCell.inMaze = true;

// Add the surrounding walls of the cell to the walls list
walls.Add(getSurroundingWalls(startingCell));

while(walls.Count != 0) {
    randomWall = removeRandomWall(walls);
    
    // Set as neighbors if only one of the cells seperated
    // by the wall is in the maze
    if (randomWall.c1.inMaze ^ randomWall.c2.inMaze) {
        setNeighbor(randomWall.c1, randomWall.c2);

        // assign cell not in the maze to the variable toAdd
        if (randomWall.c1.inMaze) toAdd = randomWall.c2;
        else toAdd = randomWall.c1;

        // Add surrounding walls of the cell not in the maze to the list
        walls.Add(getSurroundingWalls(toAdd));

        toAdd.inMaze = true;
    }
}

As we can see, the mazes generated by Randomized Depth First Search have long corridors whereas the mazes generated by Randomized Prim’s and Kruskal’s Algorithms have short corridors.

Another properly of all these algorithms is that any two cells in the maze have only one connected path, i.e., to get from one point to another you only have a single path available. This is also known as a minimum spanning tree.

If we want multiple paths to be available, we can easily achieve by removing random walls until we are satisfied.

You can find the source code for this project in this GitHub repository.